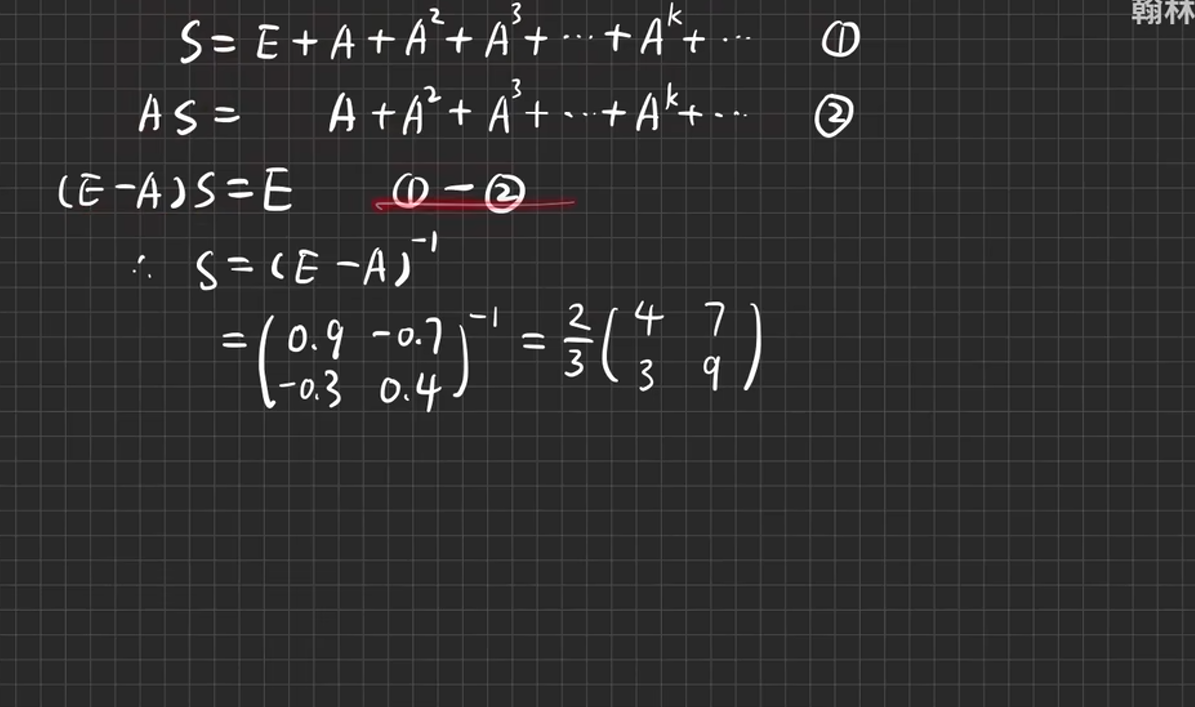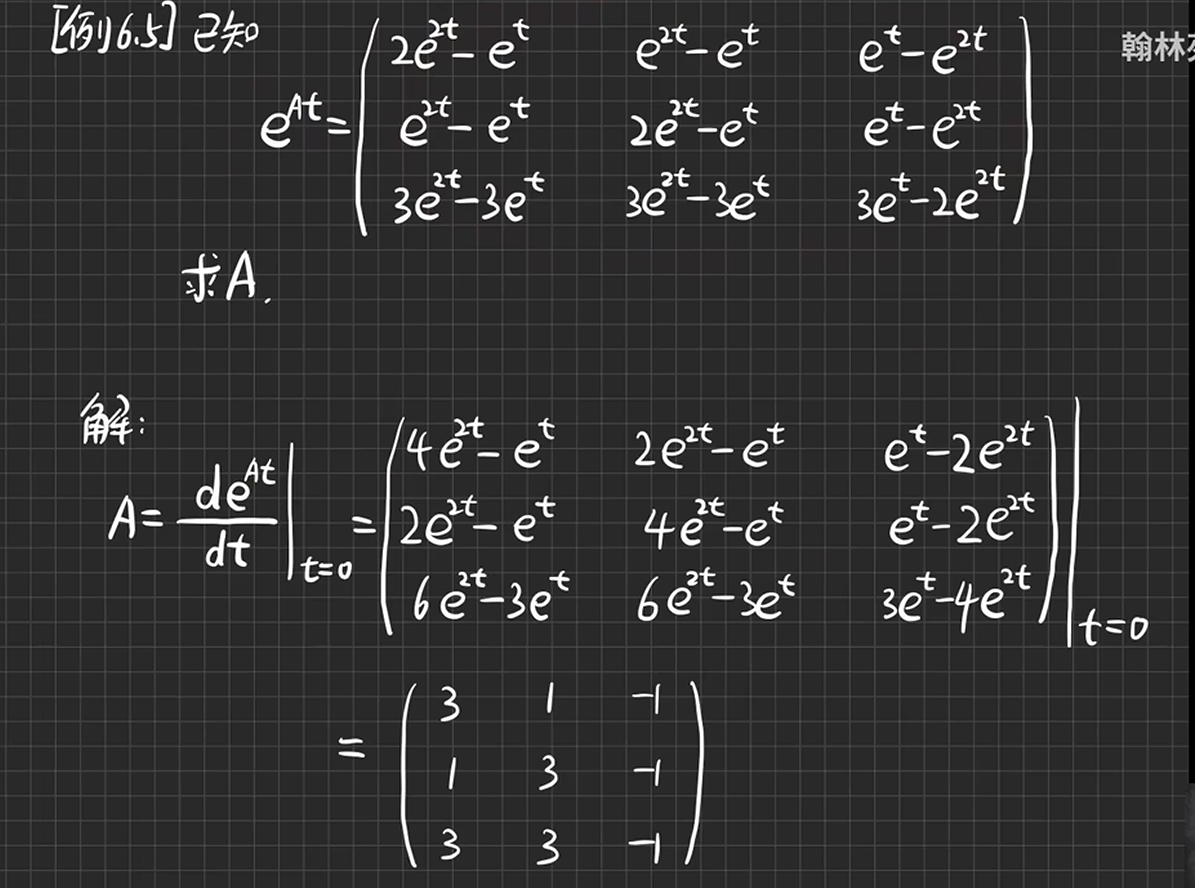矩阵论

第一章

考点一 线性空间的基与维数

补充：

数域是一个数学概念，它指的是复数集的一个非空子集，具有以下性质：

1. 包含特定的元素：数域中必须包含0和1这两个元素。
2. 封闭性：
   • 对于加法：如果a和b都是数域中的数，那么a + b也必须是数域中的数。
   • 对于减法：如果a和b都是数域中的数，那么a - b也必须是数域中的数。
   • 对于乘法：如果a和b都是数域中的数，那么a × b也必须是数域中的数。
   • 对于除法：如果a和b都是数域中的数，且b不为0，那么a ÷ b（或写作a/b）也必须是数域中的数。

换句话说，数域中的任意两个数进行加、减、乘、除（除数不为0）运算后，其结果仍然在这个数域中。

常见的数域包括：

• 复数域C：包含所有复数的集合。
• 实数域R：包含所有实数的集合，是复数域的一个子集。
• 有理数域Q：包含所有有理数的集合，即可以表示为两个整数之比的数（分母不为0），是实数域的一个子集。

需要注意的是，虽然自然数集N和整数集Z在数学中有重要地位，但它们不是数域，因为它们不满足除法的封闭性（例如，在整数集中，2除以3的结果不是整数）。

数域的概念在数学中有广泛的应用，特别是在代数、数论和高等代数等领域。它是定义和研究各种数学对象（如多项式、矩阵等）的基础之一。

例1.1

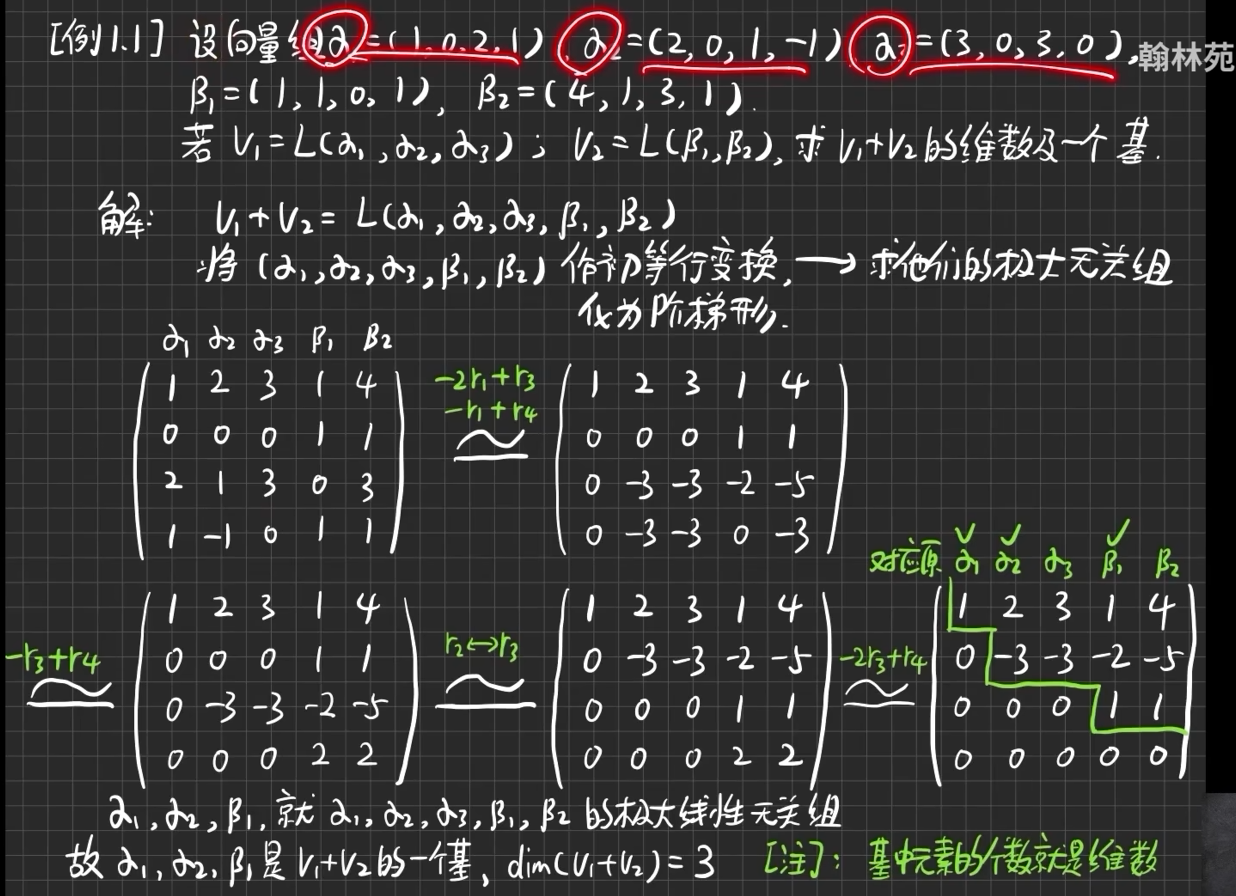
考点二 证明线性变换

例1.2

考点三 像子空间、核子空间（用线性变换定义的子空间）

考点四 线性变换矩阵

例1.3

例1.4

第二章

考点一 内积空间的定义

考点二 标准正交基

例2.1

考点三 正规矩阵的对角化

第三章

考点一 哈密顿-凯莱定理

例3.1

考点二 最小多项式

例3.2

考点三 Jordan标准型

例3.3

备注:

$$\begin{aligned} & 不变因子：\\ & d_1=1 \quad d_2=\lambda-1 \quad d_3=(\lambda-1)^2 \quad d_4=(\lambda-2)^2(\lambda-1) \\ \\ & 初级因子：\\ &\lambda-1 \quad (\lambda-1)^2 \quad (\lambda-2)^2,(\lambda-1) \\ & 约当标准型： \\ & \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 &\\ 0 & 1 & 0 & 0 & 0 & 0 &\\ 0 & 1 & 1 & 0 & 0 & 0 &\\ 0 & 0 & 0 & 2 & 0 & 0 &\\ 0 & 0 & 0 & 1 & 2 & 0 &\\ 0 & 0 & 0 & 0 & 1 & 1 &\\ \end{pmatrix} \end{aligned}$$

考点四 史密斯标准型

例3.4

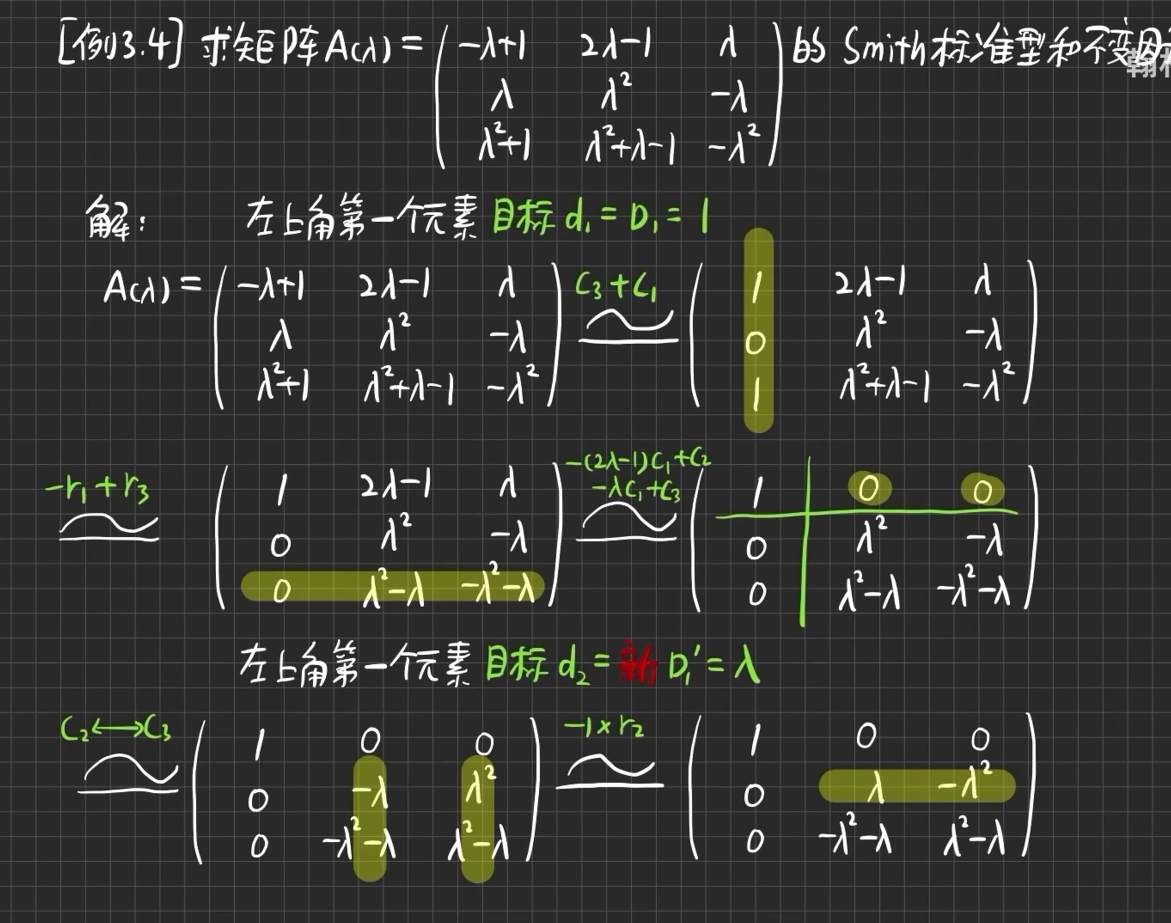
考点五 用史密斯标准型方法求解约当标准型

例3.5

第四章（不考证明题）

考点一

例4.1

考点二

矩阵范数（补充）

$$\begin{aligned} ||A||_{m1}=元素绝对值之和 \\ ||a||_F=\sqrt{元素绝对值平方之和}\\ ||A||_{m\infty}=max[行数,列数]*max(最大元素绝对值)\\ ||A||_2= \sqrt{\lambda}\quad (\lambda_1为A^HA的最大特征值)\\ ||A||_{\infty}=对每一行先绝对值再求和，取最大值 \end{aligned}$$

例4.2

第五章

例5.1

考点二

例题5.2

householder分解（补）

用例题来熟悉householder

$$\begin{aligned} & 取a_1=(1,1,-1,-1)^T,则\alpha_1=||a_1||_2=\sqrt{1^2+1^2+(-1)^2+(-1)^2}=2 \\ & u_1=\frac{a_1-\alpha_1e_1}{||a_1-\alpha_1e_1||_2}=\frac{1}{2}\begin{pmatrix} -1\\ 1\\ -1\\ -1 \end{pmatrix} \quad \quad 注：e_1=(1,0,0,0)^T\\ & H_1=\begin{pmatrix} 1 &0&0&0\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{pmatrix}-2u_1u_1^T=\frac{1}{2}\begin{pmatrix} 1 &1 &-1 &-1\\ 1 &1 &1 &1\\ -1 &1 &1 &-1\\ -1 &1 &-1 &1 \end{pmatrix}\\ & 使得\\ & H_1A=\begin{pmatrix} 2&8&0&3\\ 0&0&0&2\\ 0&0&-1&1\\ 0&4&-1&0 \end{pmatrix} \\ &又取b_2=(0,0,4)^T,则\alpha_2=||b_2||_2=4且\\ &u_2=\frac{b_2-\alpha_2\tilde{e_1}}{||b_2-\alpha_2\tilde{e_1}||_2} =\frac{1}{\sqrt{2}} \begin{pmatrix} -1\\ 0\\ 1 \end{pmatrix} \\ &于是 \\ &\tilde{H_2}=I_3-2u_2u_2^T=\begin{pmatrix} 0&0&1\\ 0&1&0\\ 1&0&0 \end{pmatrix} \\ & 令\\ & H_2=\begin{pmatrix} I_2&0^T\\ 0&\tilde{H_2} \end{pmatrix}=\begin{pmatrix} 1&0&0&0\\ 0&0&0&1\\ 0&0&1&0\\ 0&1&0&0 \end{pmatrix}\\ &H_2(H_1A)=\begin{pmatrix} 2&8&0&3\\ 0&4&-1&0\\ 0&0&-1&1\\ 0&0&0&2 \end{pmatrix}=R\\ &A=QR=(H_1H_2)R=\frac{1}{2}\begin{pmatrix} 1&-1&-1&1\\ 1&1&1&1\\ -1&-1&1&1\\ -1&1&-1&1 \end{pmatrix} \begin{pmatrix} 2&8&0&3\\ 0&4&-1&1\\ 0&0&-1&1\\ 0&0&0&2 \end{pmatrix} \end{aligned}$$

givens分解（补）

$$\begin{aligned} & 取c_1=\frac{0}{\sqrt{0^2+2^2}}=0,s_1=\frac{2}{\sqrt{0^2+2^2}}则\\ & T_{14}=\begin{pmatrix} 0&0&0&1\\ 0&1&0&0\\ 0&0&1&0\\ -1&0&0&0 \end{pmatrix}且T_{14}A=\begin{pmatrix} 2&1&1&-1\\ 0&4&0&10\\ 0&0&3&5\\ 0&-3&0&5 \end{pmatrix}\\ & 又取c_2=\frac{4}{\sqrt{4^2+(-3)^2}}=\frac{4}{5},s_2=\frac{-3}{\sqrt{4^2+(-3)^2}}=-\frac{3}{5}则\\ & T_{24}=\begin{pmatrix} 1&0&0&0&\\ 0&\frac{4}{5}&0&-\frac{3}{5}\\ 0&0&1&0\\ 0&\frac{3}{5}&0&\frac{4}{5} \end{pmatrix}且T_{24}(T_{14}A)=\begin{pmatrix} 2&1&1&-1\\ 0&5&0&5\\ 0&0&3&5\\ 0&0&0&10 \end{pmatrix}=R \\ &于是 \\ & A=QR=T_{14}^TT_{24}^TR=\frac{1}{5}\begin{pmatrix} 0&3&0&-4\\ 0&4&0&3\\ 0&0&5&0\\ 5&0&0&0 \end{pmatrix}\begin{pmatrix} 2&1&1&-1\\ 0&5&0&5\\ 0&0&3&5\\ 0&0&0&10 \end{pmatrix}\\ \end{aligned}$$

考点三 矩阵的满秩分解

例5.3（满秩分解的简便方法）

$$\begin{aligned} & 已知A=\begin{pmatrix} 0&1&-1\\ 1&0&0\\ 2&1&-1\\ 1&0&0 \end{pmatrix}求A的满秩分解。\\ & A化为行最简行列式：\\ & \begin{pmatrix} 1&0&0\\ 0&1&-1\\ 0&0&0\\ 0&0&0 \end{pmatrix}\\ &A的满秩分解为：\\ &\begin{pmatrix} 0&1\\ 1&0\\ 2&1\\ 1&0 \end{pmatrix}\begin{pmatrix} 1&0&0\\ 0&1&-1 \end{pmatrix} \end{aligned}$$

第六章

考点一 矩阵的导数

例6.1

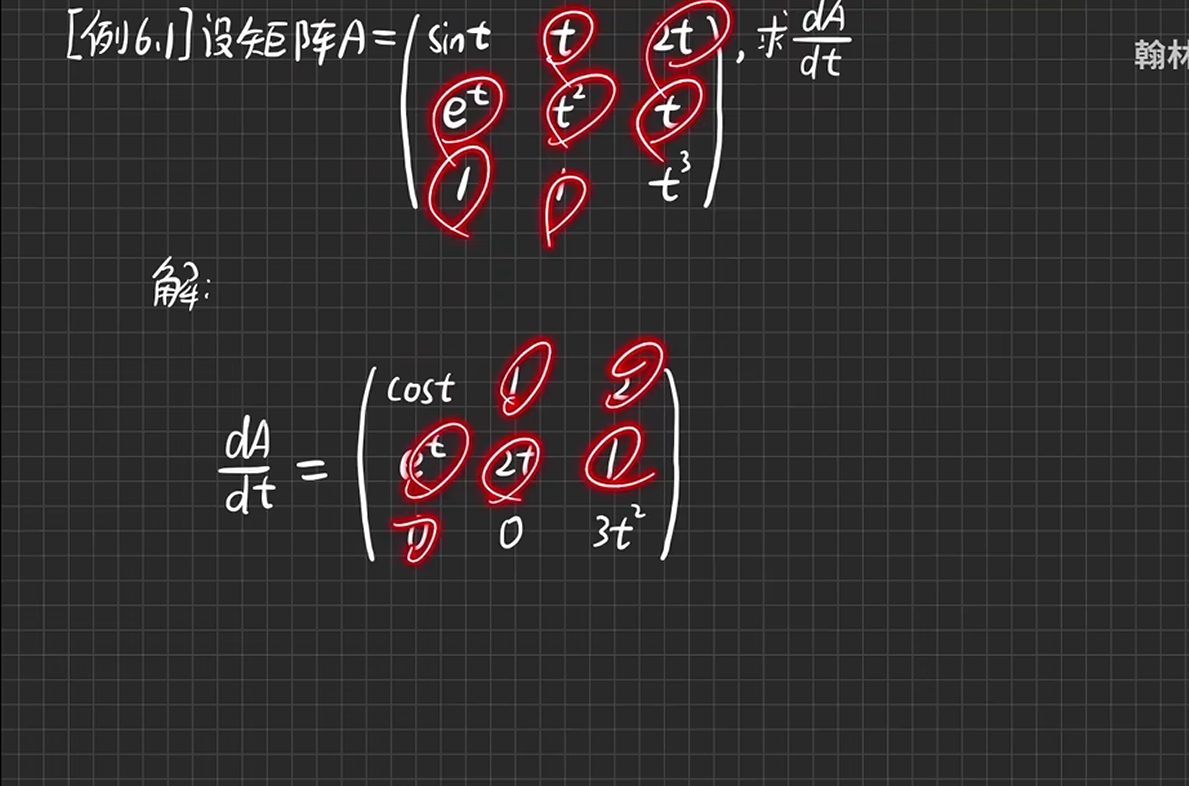
考点二 矩阵的幂级数

例6.2

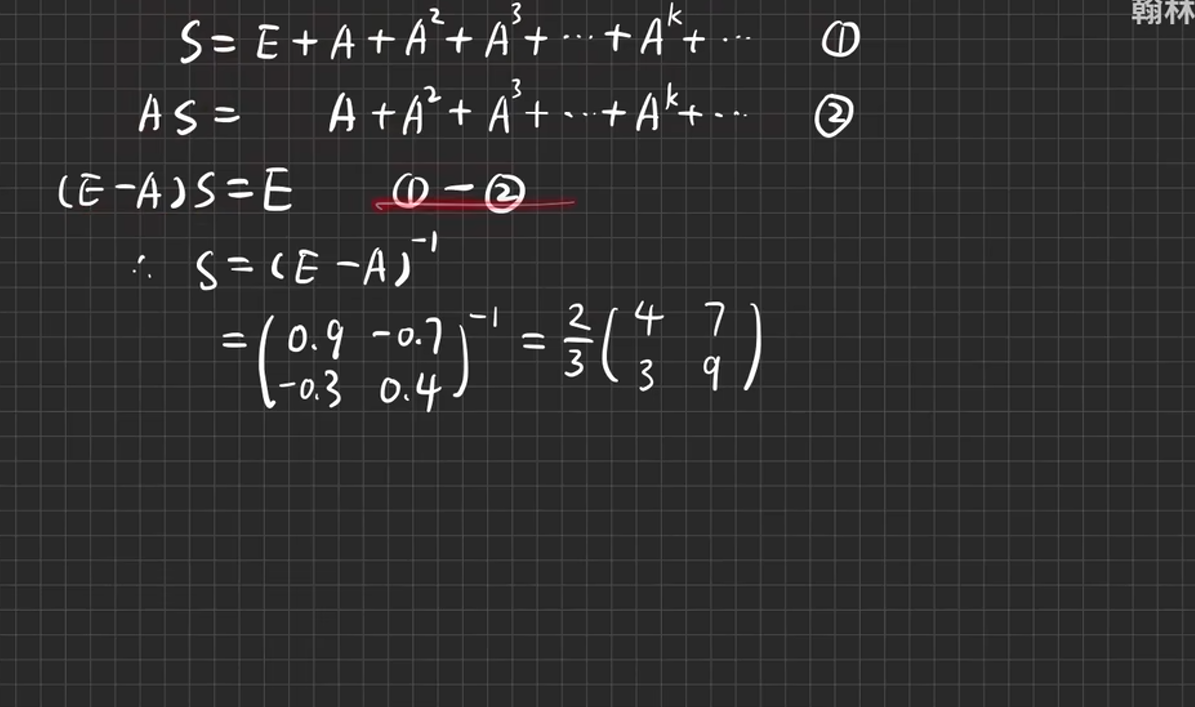
考点三

例6.3

考点四

例题 6.4

考点五

例6.5

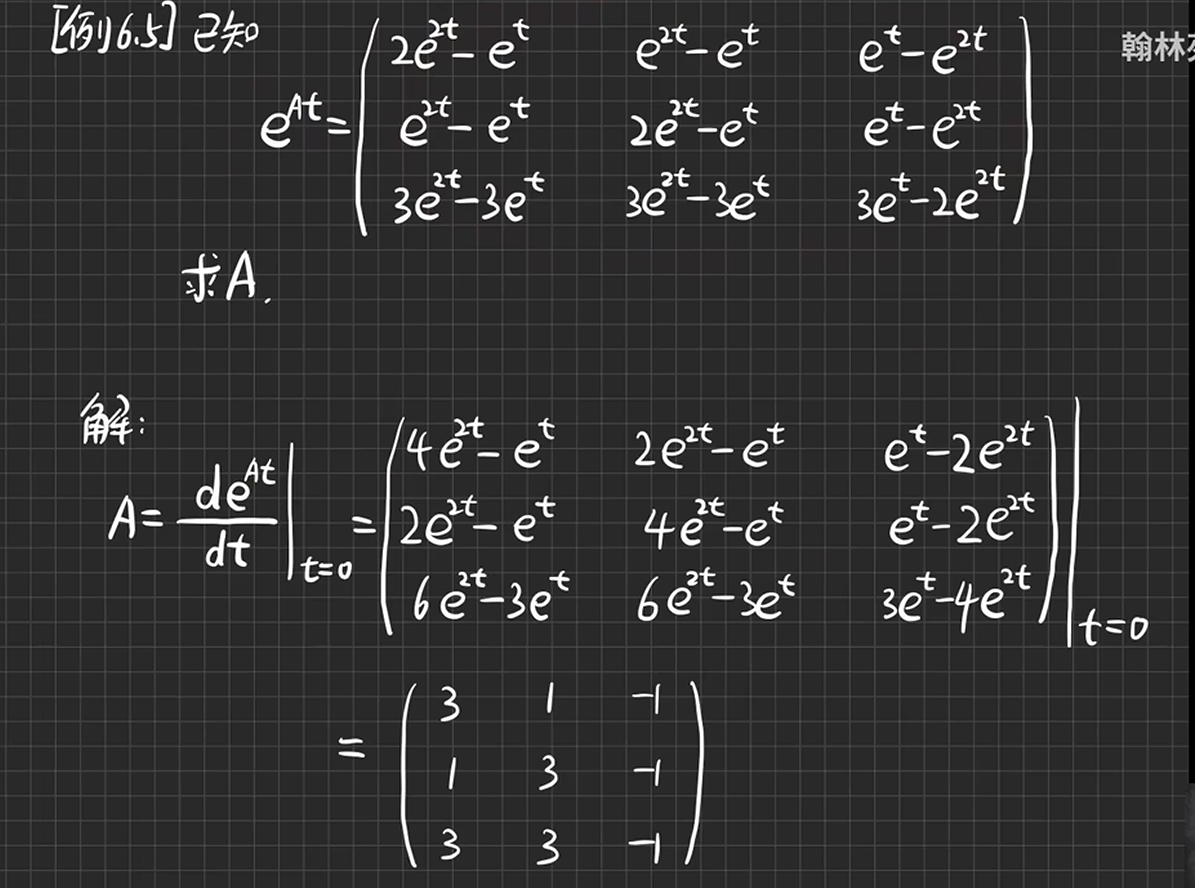
补充

正交投影矩阵

$$\begin{aligned} 对于一个向量 (\mathbf{a})，它的正交投影矩阵可以通过以下公式计算：\\ [ P_L = \frac{\mathbf{a}\mathbf{a}^T}{\mathbf{a}^T \mathbf{a}} ]\\ 计算向量(\mathbf{x} ) 沿 (L) 的投影。投影可以通过以下公式计算\\ \mathbf{p} = P_L \mathbf{x} \end{aligned}$$

盖尔圆定理

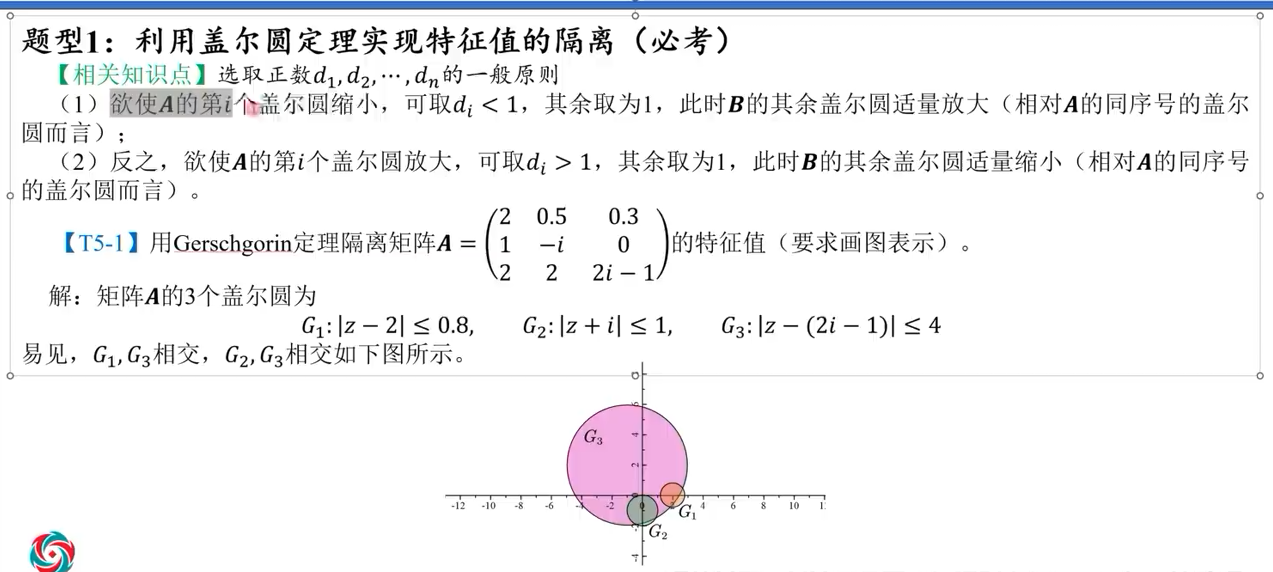
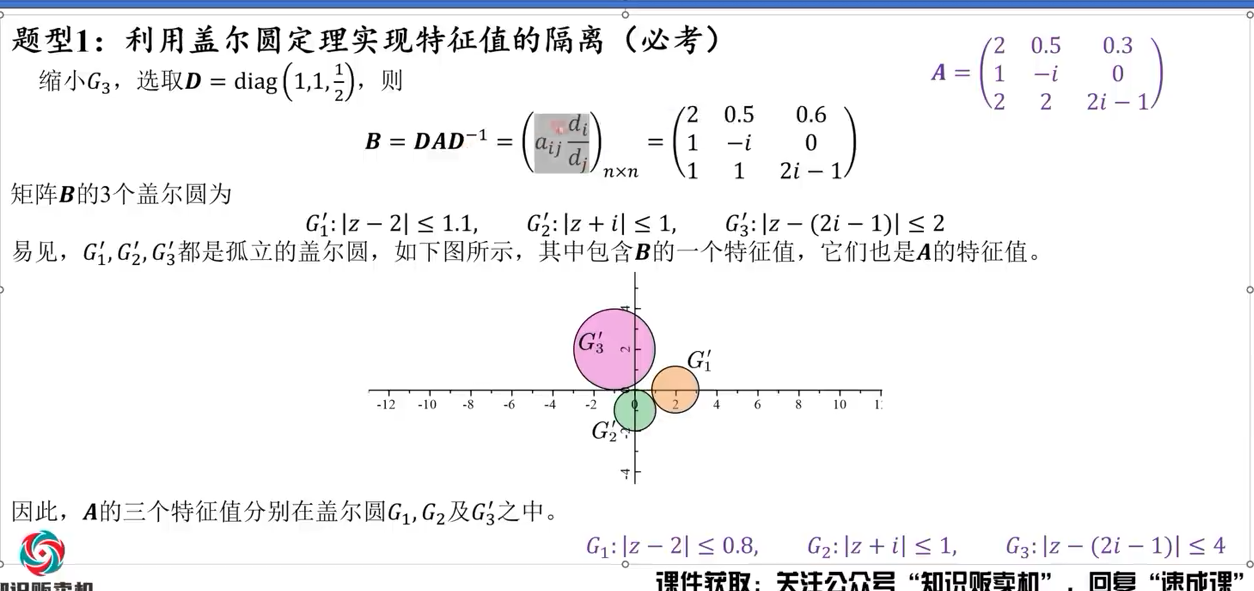
广义逆矩阵

欧式空间

一、内积（内积空间）

1.定义：

$$\begin{aligned} 设\alpha=（a_1,a_2,....,a_n）^T,\beta=(b_1,b_2,....,b_n)\in R^n,定义(\alpha,\beta)=\alpha^T\beta\\ =(\alpha_1,\alpha_2,....\alpha_n)\begin{pmatrix} \beta_1\\ \beta_2\\ ,\\ ,\\ \beta_n \end{pmatrix}=a_1b_1+a_2b_2+...+a_nb_n \end{aligned}$$

2.性质

$$\begin{aligned} (1)(\alpha,\beta)=(\beta,\alpha)\\ (2)k(\alpha,\beta)=(k\alpha,\beta)=(\alpha,k\beta)\\ (3)(\alpha+\beta,r)=(\alpha,r)+(\beta,r)\\ (4)(\alpha,\alpha)=0=\alpha=0 \end{aligned}$$

3.长度

$$\begin{aligned} |\alpha|=\sqrt{(\alpha,\alpha)}=\sqrt{a_1^2+a_2^2+....+a_n^2} \end{aligned}$$

4.正交

$$\begin{aligned} \alpha与\beta正交：(\alpha,\beta)=0 \end{aligned}$$

二、标准正交向量组

1、正交：两两正交，非0

2、标准正交：由单位向量的正交

3、正交一定线性无关，线性无关不一定正交

三、标准正交基

1、定义：

$$\begin{aligned} \alpha_1,\alpha_2,...,\alpha_n是R^n的基\\ (1)正交基：\alpha_1,\alpha_2,...,\alpha_n两两正交\\ (2)标准正交基：两两正交，且都为单位向量\\ (3)当i=j的时候，(\alpha_i,\alpha_j)=1,当i\neq j的时候，(\alpha_i,\alpha_j)=0 \end{aligned}$$

四、正交阵

$$\begin{aligned} (1)若AA^T=E,则A是正交矩阵\\ (2)|A|=1或-1\\ (3)若A可逆，A^{-1}=A^T \quad \quad (A^{-1})^T=(A^{T})^{-1}=A\\ (4)|AX|=|X|\\ (5)内积不变性：(AX,AY)=(X,Y)\\ (6)若A正交,那么A^T,A^{-1},A^*(伴随)都为正交矩阵\\ (7)若A_{n\times n}=(\alpha_1,\alpha_2,...,\alpha_n)正交方阵，\\ 则\alpha_1,\alpha_2,...,\alpha_n是R^n的标准正交基 \end{aligned}$$